En Data Sciences, la visualisation de données une étape qui intervient tout au long d’un projet : aussi bien dans la phase de recherche et d’analyse, que dans la présentation finale pour le client. Il est donc indispensable de connaitre les techniques de visualisation les plus utiles et de savoir comment interpréter ces graphiques. Je vous propose donc de découvrir 5 graphiques utiles avec Matplotlib !

Scatter : Les Nuages de points

Commençons par la base de la base : les nuages de points. Ces graphiques sont les plus simples à créer et à interpréter. Ils sont très utiles pour détecter toute tendance linéaire ou polynomiale entre 2 variables de votre Dataset. Pour les réaliser avec Matplotlib, je vous recommande d’utiliser la fonction plt.scatter.

Le gros désavantage, c’est qu’il n’est pas facile d’observer la relation entre plus de 2 variables à la fois, mais le code ci-dessous vous dévoile une petite astuce pour observer la relation entre plusieurs variables sur une seule figure.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

# chargement d'un dataset de fleur d'iris
iris = load_iris()
X = iris.data # X contient 150 échantillons, 4 variables
y = iris.target # y contient 150 échantillons, 3 classes

# création d'une boucle for pour afficher tous les graphiques
n = X.shape[1]
plt.figure(figsize=(12, 8))
for i in range(n):
    plt.subplot(n//2, n//2, i+1)
    plt.scatter(X[:, 0], X[:, i], c=y) # affiche la variable i en fonction de la variable 0
    plt.xlabel('0')
    plt.ylabel(i)
    plt.colorbar(ticks=list(np.unique(y)))
plt.show()
<p>

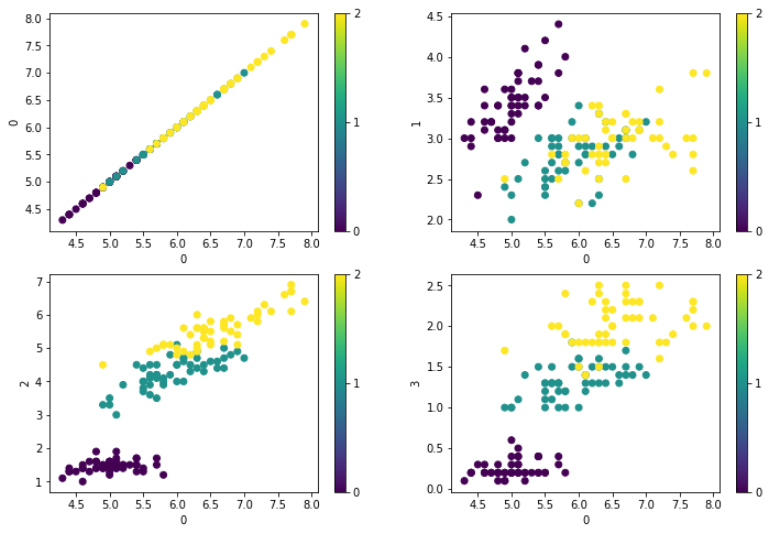
Astuce : Pour créer ce genre de graphique, Il est bien plus rapide et efficace d’utiliser une autre librairie appelée Seaborn. La fonction sns.pairplot() procure de meilleurs résultats que l’exemple ci-dessus !

Graphiques 3D

3D Scatter avec Matplotlib

Les graphiques 3D sont également incontournables en Data Science et mathématiques. Évidemment, leur but premier est d’étendre les graphiques 2D (comme ceux du dessus) pour visualiser les relations entre 3 variables à la fois. Pour créer des graphiques 3D, il faut commencer par charger le module 3D de Matpotlib (mplot3d) et son objet Axes3D. Ensuite, il faut créer un objet axe avec une projection 3D, ce qui ouvre la possibilité de tracer des surfaces, des nuages de points, des lignes, et d’autres style de graphiques 3D.

%matplotlib # cette ligne permet d'ouvrir une fenêtre QT5 pour zoomer et bouger votre graphique !
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # module 3D de Matplotlib

ax = plt.axes(projection='3d') # Création d'un objet "axe 3D"
ax.scatter(x[:, 0], x[:, 1], x[:,2], c=y)
<p>

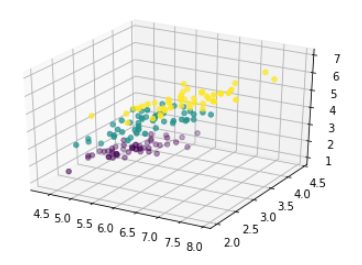
A présent je dois vous prévenir : les graphiques 3D ne sont pas très utiles en Data Science et en Machine Learning. Voici 2 arguments permettant de justifier cette affirmation :

• Face à un Dataset à des centaines de dimensions, un graphique 3D ne fait guère mieux qu’un graphique 2D en terme de représentation. Idéalement il faudrait utiliser des graphiques à 1000 dimensions, mais cela n’existe pas.
• les graphiques 2D sont plus faciles à interpréter que les graphiques 3D. D’ailleurs on se ramène souvent aux projections 2D quand on utilise des graphiques 3D (ce sont les contourplots)

Cependant, je réserve aux graphiques 3D une utilité toute particulière : celle d’impressionner vos collègues dans le cas où vous devez représenter des fonctions mathématiques avec des surfaces

3D surfaceplot

Les graphiques 3D ont tout même une place importante en mathématiques et en physique. Ils sont très utile pour représenter des surfaces et des fonctions à 2 paramètres.

latexpage

Imaginez vouloir observer la surface générée à partir de la fonction f(x, y) = sin(x) + cos(y) sur un domaine de x, y \in [0, 5]. Pour cela, il faut calculer chaque valeur de f(x, y) sur une grille (X, Y) à 2 dimensions. Cette grille 2D est couramment appelée meshgrid en ingénierie et mathématiques. Pour la créer, il faut passer les valeurs de x, y dans une fonction numpy appelée np.meshgrid(x, y). Ensuite, on peu tracer la surface f(X, Y) en fonction de X et Y avec la fonction surface_plot.

# Création d'une fonction
f = lambda x, y: np.sin(x) + np.cos(y)

# Création d'un domaine d'étude X, Y
x = np.linspace(0, 5, 100)
y = np.linspace(0, 5, 100)
X, Y = np.meshgrid(x, y)

# Résultat : tableau numpy 2D
Z = f(X, Y)

# Affichage de la surface
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, cmap='plasma')
<p>

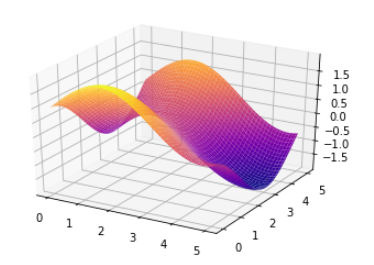
Astuce : Si vous utiliser Jupyter Notebook, ajoutez %matplotlib au début de votre code pour afficher le graphique dans une fenêtre à part, ce qui permet de zoomer, et tourner votre graphique 3D !

Histogrammes Matplotlib

L’histogramme est le graphique idéal pour visualiser la répartition de vos données selon une ou plusieurs variables quantitatives. En statistiques, c’est ce qu’on appelle visualiser une distribution. Le principe est simple : il s’agit de créer plusieurs intervalles entre le minimum et le maximum de vos données pour ensuite compter le nombre d’échantillons qui sont compris entre chaque intervalle. Voici par exemple un histogramme présentant le nombre (ou la fréquence) d’individus entrant dans différentes catégories d’age :

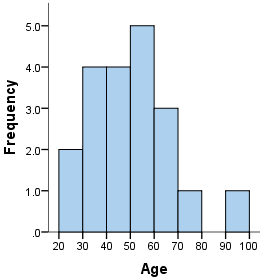
Dans toute analyse de données, on commence par utiliser des histogrammes pour visualiser la distribution de nos données : Quel est le poids de nos individus ? Quel est le prix des appartements du dataset ? Bien souvent, on obtient un histogramme avec une allure de cloche de Gauss, signe que nos données sont distribuées de façon normale, mais d’autres types de distributions ne sont pas rares (distribution uniforme ou logarithmique).

Pour créer un histogramme avec Matplotlib, il faut utiliser la fonction plt.hist(). Dans cette fonction, il faut passer un tableau Numpy à une dimension. Veillez donc à ne sélectionner qu’une colonne dans votre dataset, ou penser a utiliser la méthode nd.ravel() pour “aplatir” vos tableaux Numpy.

Pour tracer un bel histogramme, Il est important de définir le nombre d’intervalles à utiliser. Pour cela, il faut utiliser l’argument bins. Je vous conseille de tester différents nombres d’intervalles. Voici un exemple d’utilisation :

# Générations de données : 1000 points aléatoires normaux
x = np.random.randn(1000)

# visualisation sur 50 intervalles
plt.hist(x, bins=50)
<p>

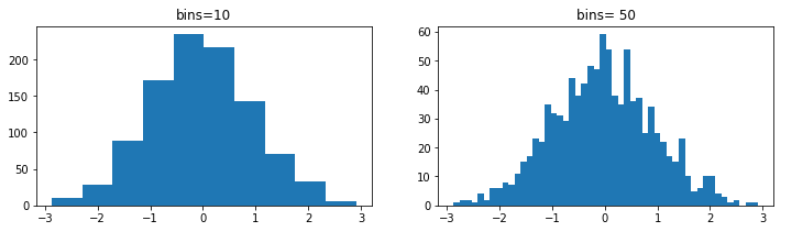
Astuce: Écrivez plt.hist(x, bins=x.size) pour construire un histogramme où chaque intervalle correspond en réalité à une valeur. Si votre dataset est très large, divisez plutôt x.size par un nombre: bins=x.size//10 pour créer moins d’intervalles. Cette astuce est très utile pour analyser les pixels d’une photo !

Contour plots Matplotlib

Les contour plots sont des graphiques utiles et simples à interpréter. Ils représentent une vue du dessus des graphiques 3D. Semblables à une carte de relief, où les différents niveaux d’altitude sont représentés par des contours, on les utilise pour visualiser des fonctions mathématiques et trouver à l’œil un minimum ou maximum.

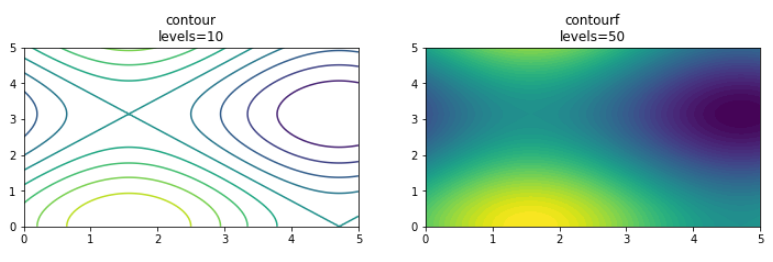
Ces graphiques se construisent sur la même base qu’un graphique 3D : il faut créer un tableau 2D de nos axes X, Y avec la fonction meshgrid, puis utiliser ces tableau dans la fonction plt.contour() ou contourf(). l’argument levels permet de tracer la fonction de contour avec plus ou moins de niveau d’altitudes.

X = np.linspace(0, 5, 100)
Y = np.linspace(0, 5, 100)
X, Y = np.meshgrid(X, Y)

Z = f(X, Y)

plt.contour(X, Y, Z, levels=40)
<p>

Imshow Matplotlib

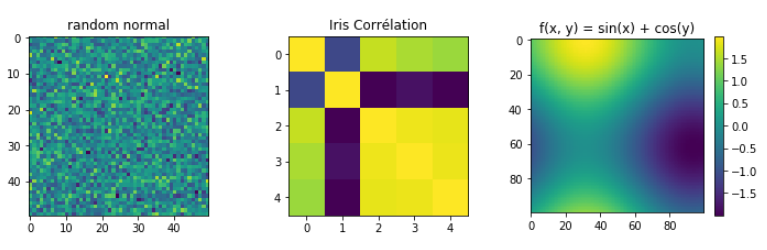
Pour finir, les graphiques imshow() de Matplotlib comptent parmi les plus utiles de toute la data science. Il s’agit tout simplement d’afficher une matrice 2D de la même façon que les pixels d’une image 2D. On peut ainsi visualiser des matrices de confusion, des matrices creuses, des images, ou même des contour plots avec imshow() ! Pour utiliser cette fonction, il suffit de lui fournir un tableau Numpy 2D :

plt.figure(figsize=(12, 3))

# Simple graphique imshow()
X = np.random.randn(50, 50)

plt.subplot(131)
plt.imshow(X)

# Matrice de corrélation des iris
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target

plt.subplot(132)
plt.imshow(np.corrcoef(X.T, y))

# Matrice f(X, Y) = sin(X) + cos(Y)
X = np.linspace(0, 5, 100)
Y = np.linspace(0, 5, 100)
X, Y = np.meshgrid(X, Y)

plt.subplot(133)
plt.imshow(f(X, Y))
plt.colorbar()
<p>