La Descente de Gradient, (ou Gradient Descent en anglais) est un des algorithmes les plus importants en Machine Learning et en Deep Learning. il s’agit d’un algorithme d’optimisation extrêmement puissant et scalable qui permet d’entraîner de nombreux modèles comme ceux de régression linéaire, de régression logistiques ou encore les réseaux de neurones. Si vous vous lancez dans le Machine Learning, il est donc impératif de comprendre en profondeur l’algorithme de la descente de gradient, et après avoir lu cet article, ça sera chose faite !
La Descente de Gradient, qu’est-ce-que c’est ?
La Descente de Gradient est un algorithme d’optimisation qui permet de trouver le minimum de n’importe quelle fonction convexe en convergeant progressivement vers celui-ci.
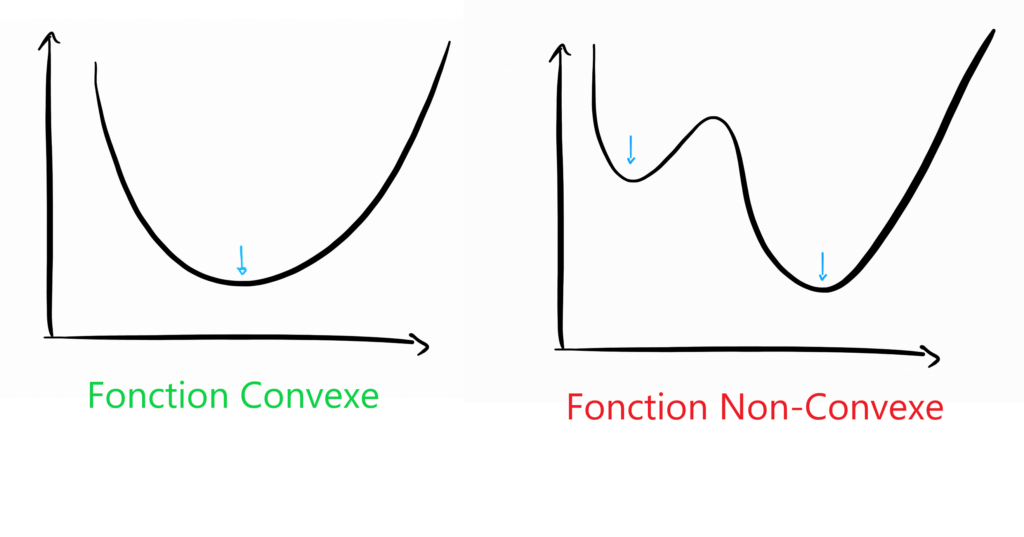
Note : Une fonction convexe est une fonction dont l’allure ressemble à celle d’une belle vallée avec au centre un minimum global. A l’inverse, une fonction non-convexe est une fonction qui présente plusieurs minimums locaux et l’algorithme de descente de gradient ne doit pas être utilisé sur ces fonctions, au risque de se bloquer au premier minima rencontré.
Pourquoi la Descente de Gradient est si importante en Machine Learning ?
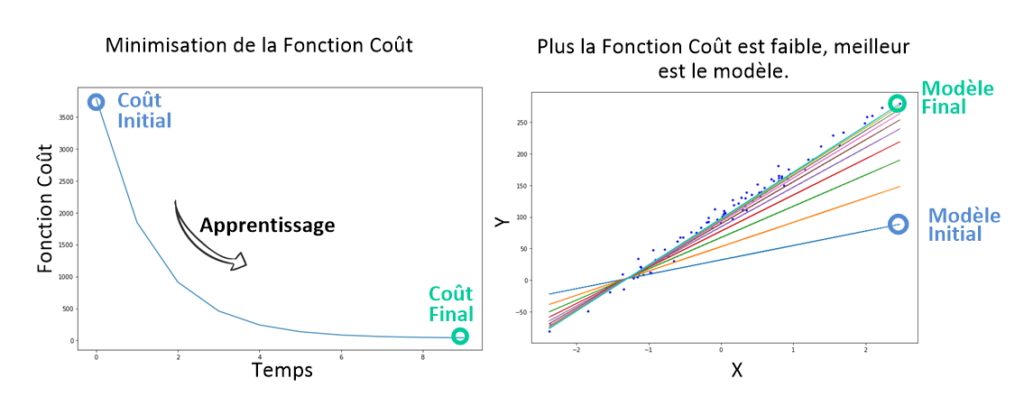
En Machine Learning, on va utiliser l’algorithme de la Descente de Gradient dans les problèmes d’apprentissage supervisé pour minimiser la fonction coût, qui justement est une fonction convexe (par exemple l‘erreur quadratique moyenne).
C’est grâce à cet algorithme que la machine apprend, c’est-à-dire trouve le meilleur modèle. En effet, rappelez-vous que minimiser la fonction coût revient à trouver les paramètres a, b, c, etc. qui donnent les plus petites erreurs entre notre modèle et les points y du Dataset. Une fois la fonction coût minimisée, c’est le Jackpot ! À nous les programmes de reconnaissance vocale, de vision par ordinateur, et les applications pour prédire le cours de la bourse !
Vous comprenez donc pourquoi l’algorithme de Gradient Descent est fondamental: La machine apprend grâce à lui.
Pour vous expliquer son fonctionnement, je vais commencer par vous donner une analogie que tout le monde peut comprendre, après quoi je rentrerai à fond dans les maths.
Perdu en montagne, comment retrouver son chemin ?
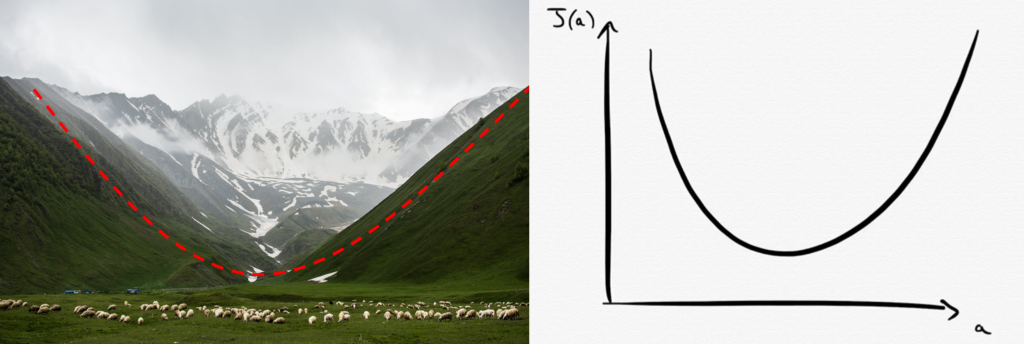
Imaginez que vous soyez perdu en pleine montagne. Votre but est de rejoindre un refuge situé au point le plus bas de la vallée dans laquelle vous vous situé. Le problème, c’est que vous n’avez pas pris de carte avec vous et vous ignorez donc complètement les coordonnées de ce refuge. Vous devez vous débrouiller tout seul…
Ne vous en faites pas, car voici une stratégie en 2 étapes qui va vous permettre de vous en sortir !
- Depuis votre position actuelle, vous cherchez tout autour de vous la direction de là où la pente descend le plus fort.
- Une fois que vous avez trouvé cette direction, vous la suivez sur une certaine distance (disons que vous marchez 300 mètres) puis vous répétez l’opération de l’étape 1.
En répétant ainsi les étapes 1 et 2 en boucle, vous êtes sûr de converger vers le minimum de la vallée. Eh bien cette stratégie n’est ni plus ni moins que l’algorithme de la Descente de Gradient !

Mais vous ? Que feriez-vous si vous étiez perdus en Montagne ? Dites-le-moi en commentaire ! 🙂
Descente de Gradient : De la Montagne au Machine Learning
En machine Learning, la vallée dans laquelle nous nous situons est en fait la Fonction Coût $J$. On peut répéter en boucle les deux étapes vues précédemment pour en trouver le minimum !
Étape 1 : Calcul de la dérivée de la Fonction Coût
Nous partons d’un point initial aléatoire (comme si nous étions perdus en montagne) puis nous mesurons la valeur de la pente en ce point. Et comment mesure-t-on une pente en mathématique ? En calculant la dérivée de la fonction !
Note : Gradient et dérivée peuvent être perçus comme étant la même chose. En fait le gradient est la généralisation vectorielle de la dérivée. Mais vraiment, c’est la même chose.
Étape 2 : Mise à jour des paramètres du modèle
On progresse ensuite d’une certaine distance $\alpha$ dans la direction de la pente qui descend, mais pas 300 mètres cette fois-ci ! On appelle cette distance Learning Rate, que l’on pourrait traduire par vitesse d’apprentissage.
Cette opération a pour résultat de modifier la valeur des paramètres de notre modèle (nos coordonnées dans la vallée changent quand on se déplace).
Descente de Gradient : Un algorithme itératif
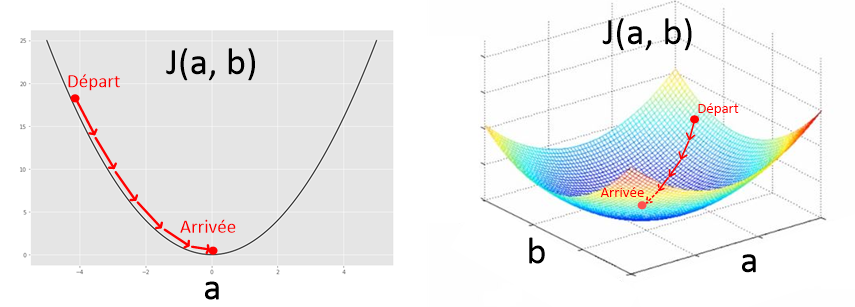
En répétant ces deux étapes en boucle, l’algorithme de Gradient Descent est donc un algorithme itératif. Pour l’illustrer sur un graphique, je vais prendre l’exemple de la fonction coût $J(a, b)$ que l’on a développé pour une régression linéaire. L’algorithme permet de trouver la valeur idéale pour les paramètres $a$ et $b$.
En résumé, voici les liens entre l’analogie de la montagne et le Machine Learning :
| Analogie de la montagne | Machine Learning |
| Vallée convexe | Fonction Coût |
| Pente de la vallée | Dérivée de la Fonction Coût |
| Distance parcourue (300 mètres) | Learning Rate multiplié par la dérivée |
| Coordonnées initiales (nous sommes perdus) | Paramètres initiaux (choisis au hasard) |
| Coordonnées du refuge | Les paramètres qui donnent le meilleur modèle |
Comment implémenter l’algorithme de la Descente de Gradient ?
Pour implémenter cet algorithme, c’est très simple ! il suffit d’écrire la ligne suivante et Magie le paramètre $a$ convergera vers le minimum de $J(a, b)$. On fera la même chose pour le paramètre $b$ !
a = a - \alpha \frac{\partial J(a, b) }{ \partial a}
En fait, ça n’a rien de magique. Je vais vous expliquer comment une simple ligne nous permet d’obtenir la descente de gradient observée sur le graphique précédent.
Lorsque l’algorithme commence au tour $i=0$, nous pouvons calculer la position $a_1$ en appliquant la formule :
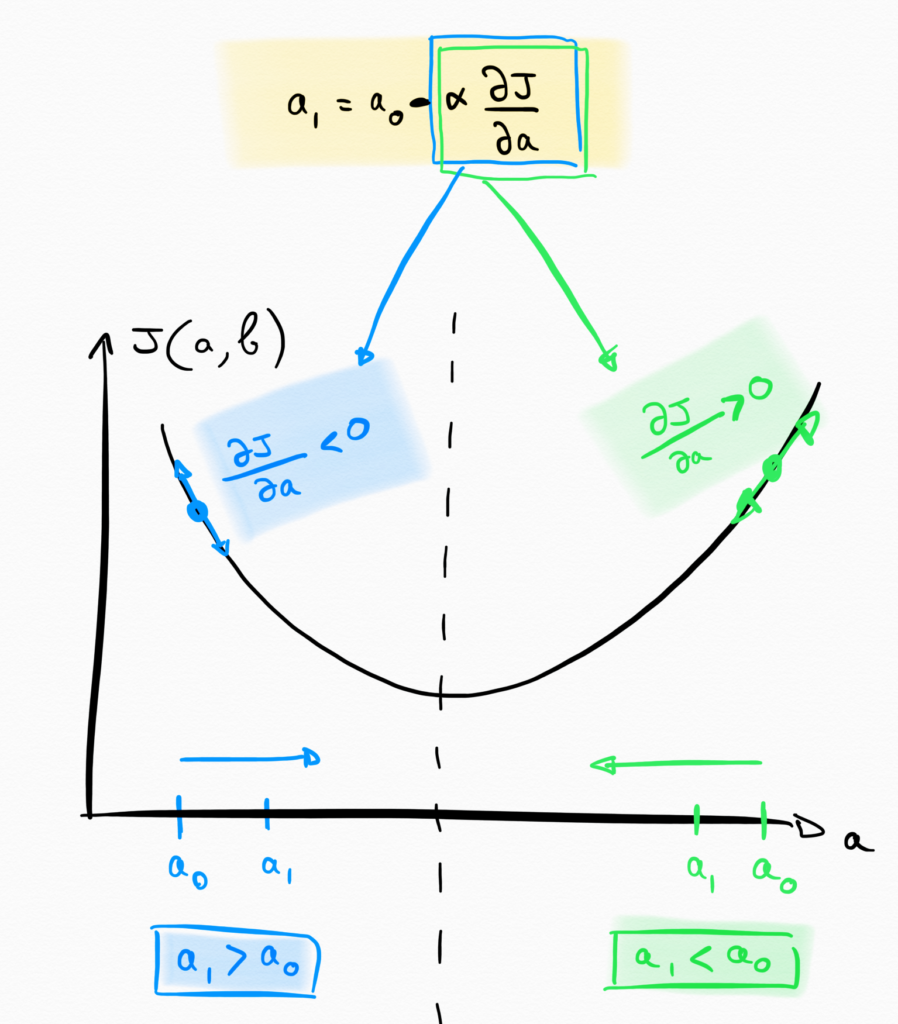
a_1 = a_0 - \alpha \times \frac{\partial J(a, b)}{ \partial a}
Dans le cas où a_0 se situe à gauche de notre minimum, la dérivée \frac{\partial J(a, b)}{ \partial a} sera négative (car vous voyez bien que vous êtes sur une pente descendante. $\alpha$ étant toujours positif, le produit \alpha \times \frac{\partial J(a, b)}{ \partial a} est négatif, donc on a a_1 = a_0 - truc_{negatif} ce qui revient à a_1 = a_0 + truc_{positif}. Ainsi on a a_1 > a_0, ce qui a pour résultat se déplacer vers la droite.
A l’inverse, si a_0 se situe de l’autre côté de la vallée, alors la dérivée sera cette fois positive, et par déduction vous trouverez que a_1 < a_0, ce qui a pour résultat que $a$ se déplace vers la gauche du graphique.
Maintenant que vous connaissez la formule de la descente de gradient, il ne reste plus qu’à l’utiliser pour minimiser les Fonctions Coûts de votre choix. Le calcul des dérivés partielles \frac{\partial J(a, b)}{ \partial a} et \frac{\partial J(a, b)}{ \partial b} dépendra donc du problèmes sur lequel vous travaillez.
Dans la dernière partie de cet article, je vous propose donc de voir comment calculer les dérivées partielles de l’erreur quadratique moyenne, ce qui vous permettra d’utiliser la descente de gradient pour résoudre des problèmes de régression linéaire.
Application : Descente de Gradient pour Régression linéaire
Pour appliquer la descente de gradient sur un problème de régression linéaire, il faut calculer le gradient de l’erreur quadratique moyenne :
J(a, b) = \frac{1}{2m} \sum_{i = 1}^{m}(ax^{(i)} + b - y^{(i)})^2.
Pour faire simple, je vais détailler le calcul des dérivées partielles de cette fonction en 3 étapes.
Note: Pour vous aider à comprendre les explications qui suivent, je vous invite a regarder la vidéo en haut de page.
1. Exprimer la fonction coût en tant que fonction composée
Pour mener à bien ce calcul, il faut commencer par décomposer cette fonction en 2 fonctions $g$ et $f$ :
f(a, b) = ax + b - y
g(f) = f^2
On a alors :
J(a, b) = \frac{1}{2m} \sum g \circ f(a, b)
Pour calculer le gradient en $a$, on pourra écrire que:
\frac{\partial J(a, b)}{ \partial a} = \frac{1}{2m} \sum \frac {\partial g \circ f(a, b)}{\partial a}
2. Dérivée de la fonction composée
L’étape suivante est le calcul de la dérivée \sum \frac {\partial g \circ f(a, b)}{\partial a} .
Pour rappel, voici la formule pour dériver une fonction composée (g \circ f(x))’ = f’(x) \times g’ (f(x))
En dérivant cette fonction, on obtient donc :
\frac{\partial J(a, b)}{\partial a} = \frac{1}{m} \sum_{i = 1}^{m} x^{(i)} \times (ax^{(i)} + b - y^{(i)})
Note: (le carré de la fonction g est tombé, et s’est simplifié avec le \frac{1}{2m} et le coefficient x^{(i)} provenant de f(a, b) est sorti.
3. La dérivée partielle par rapport à b
Pour le calcul du gradient selon le paramètre b, on a le même résultat au facteur x^{(i)} prêt, ce qui donne :
\frac{\partial J(a, b)}{\partial b} = \frac{1}{m} \sum_{i = 1}^{m} (ax^{(i)} + b - y^{(i)})
Vous voulez une 3ième bonne nouvelle ? Maintenant que vous disposez des calculs pour les deux gradients, il suffit de les entrer dans l’algorithme de la descente de gradient, et la machine va commencer à apprendre ! Oui ! Vous avez ENFIN écrit votre premier algorithme de Machine Learning en entier. Félicitations ! Remarquez au passage que le tout ne tient qu’en quelques lignes…

Learning Rate : le rôle de l’hyper-paramètre alpha
Avant de conclure cet article, je dois vous parler du Learning Rate $\alpha$. En Machine Learning, on appelle ce genre de facteur un Hyper-paramètre, parce qu’il n’est pas à proprement parler un paramètre de notre modèle, mais il a tout de même un impact sur la performance finale de notre modèle (tout comme les paramètres du modèle). Je vous explique pourquoi.
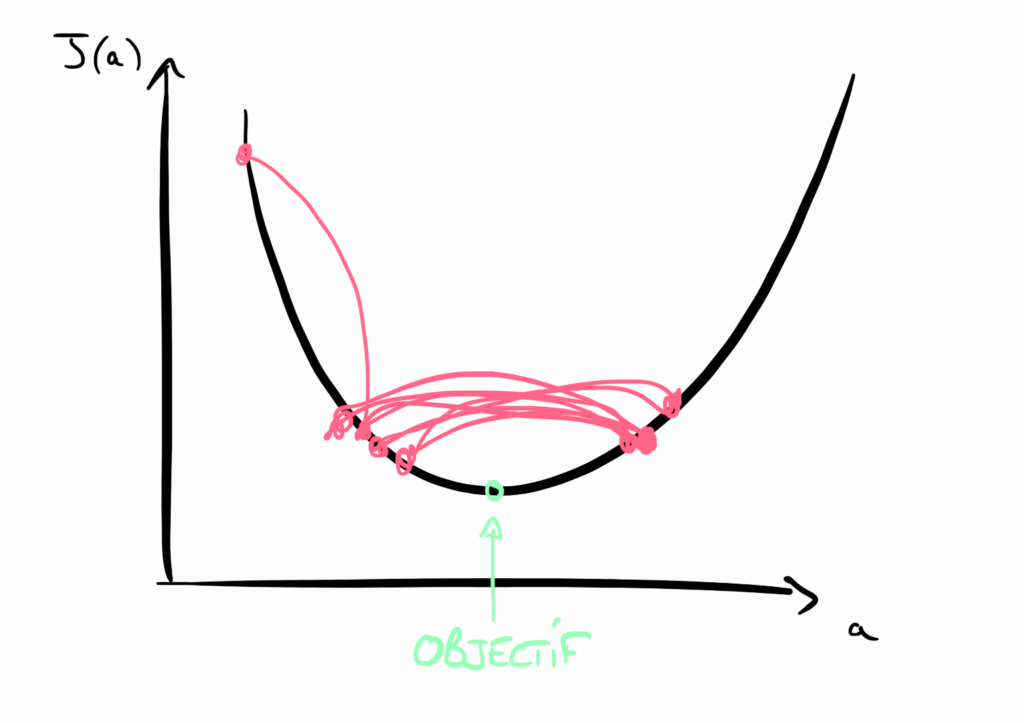
Learning Rate trop grand
Si le Learning Rate est trop grand, alors vous ferez de trop grands pas dans la descente de gradient. Cela a l’avantage de descendre rapidement vers le minimum de la fonction coût, mais vous risquez de louper ce minimum en oscillant autour à l’infini… Dommage. Dans l’analogie de la vallée, c’est comme si vous vous déplaciez à chaque fois de plusieurs kilomètres, en dépassant ainsi le refuge sans vous en rendre compte !
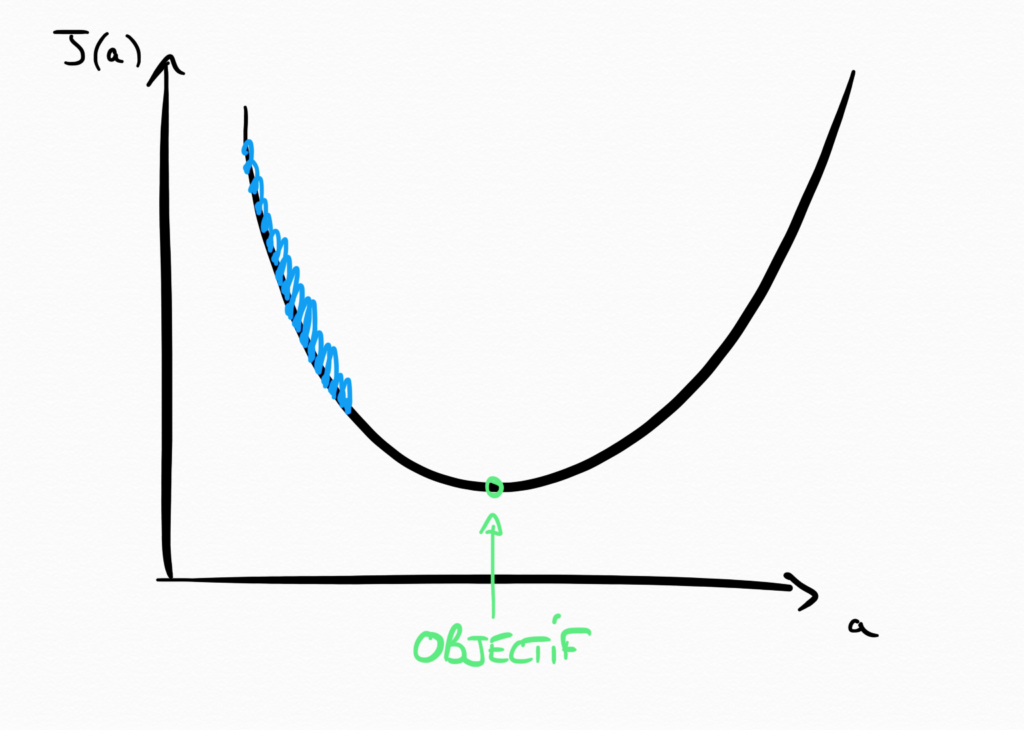
Learning Rate trop petit
Pour éviter le cas précédent, vous pourriez être tenté de choisir un Learning Rate très faible. Mais s’il est trop faible, alors vous risquez de mettre un temps infini avant de converger vers le minimum de la fonction cout. C’est un peu comme choisir d’avancer millimètre par millimètre dans la montagne pour trouver le point le plus bas de la vallée. Bonne chance !
Comment trouver la bonne valeur pour votre hyper-paramètre alpha ?
Pour trouver le bon Learning Rate, il n’existe malheureusement pas de formule magique. Le plus souvent, on doit tâtonner et essayer plusieurs valeurs avant de trouver la bonne. On appelle ça l’Hyperparameter Tuning (le réglage des hyper-paramètres) et nous verrons plus tard dans cette formation les différentes stratégies pour bien effectuer ce réglage.
Néanmoins, un bon Learning Rate se situe souvent aux alentours des \alpha = 0.001.
Votre premier algorithme de Machine Learning enfin complet !
Je vous remercie d’avoir suivi les 4 premiers articles de cette formation de Machine Learning. Il y a encore quelques jours, vous ignoriez peut-être tout du Machine Learning, et vous savez désormais écrire un algorithme de régression linéaire !
Alors avant que nous passions à l’étape suivante, je vous invite à prendre du recul et à vous féliciter. J’insiste ! Vous faites déjà partis des meilleurs, car avez compris la mécanique qui fait fonctionner l’apprentissage supervisé (Dataset – Modèle – Fonction Coût – Gradient Descent) et vous savez la mettre en pratique. Bravo !






Bonjour, très bon article. Il y a une erreur de formule au chapitre 1 non ? a1 = a0 – truc négatif soit a1 = a0 + truc positif !
Merci Gaetan ! Le signe négatif a en effet sauté. je le rajoute !
bonjour,j’aime bien votre cours car il est facile a comprendre pour un débutant merci beaucoup.J’ai une question,quelle notion en mathématique doit-on avoir pour les machines learning ?
Pour comprendre les bases du Machine Learning, il suffit de connaitre les bases du calcul (surtout les dérivées composées) les bases sur les matrices (multiplications, additions, transposée) et les bases des statistiques (distributions, maximum de vraisemblance)
Ensuite, pour avoir un niveau plus élevé, il faut bien maitriser l’algebre linéaire (valeur propres etc) et meilleur vous êtes en statistiques, meilleur vous serez en Data Science.
Bonjour Guillaume Saint-Cirgue
mercis infiniment grâce a vous je me suis aprende ML encore mieux améliorer
je vais développer un programme de ML.
1) comment déterminer les variables (x,y) dataset d’une courbe physique (exemple photovoltaïque I-V ou
P-V))pour remplir le tableau dataset et extraire le point maximal?
2)j’aimerai avoir un tutoriel comment utilise big data en python?
très facile à comprendre !!
merci pour les cours !!
Merci Guillaume pour ta formation, elle m’a été d’une grande utilité… J’aimerais que tu publies d’autres livres si possible qui nous aiderons une fois de plus
Bonjour!
Très bon article!
Bonjour Guillaume,
Vraiment un grand bravo pour ce tutoriel qui est le plus didactique sur le sujet que j’ai trouvé !
Après des recherches sur de multiples sites qui m’avaient découragé par leur explication trop brève sur la descente de gradient ou trop compliquée, je suis enfin tombé sur cette pépite de tutoriel. Et je peux dire que j’en ai visité des sites !
Depuis ce tutoriel, j’ai pratiquement terminé de voir toutes tes vidéos sur le machine learning. Un grand bravo et merci !
Hâte d’avoir la suite sur le deep learning 🙂 et sur les statistiques de ce que j’ai compris récemment.
Si je peux me permettre de te donner un conseil, c’est de continuer dans ces explications hyper détaillées sur les boites noires que sont les algorithmes. Je pense que c’est le petit plus qui te démarque des autres sites/tutoriels sur internet.
Je te dis ça parce que j’ai trouvé que l’explication sur la régression logistique sur ton livre (et vu que tu n’as pas fait de vidéos sur youtube sur le sujet) était un peu trop succincte. Il aurait été intéressant de faire une comparaison avec la régression linéaire parce que je t’avoue que je me suis tiré les cheveux à comprendre pourquoi on utilisait la fonction sigmoide, l’utilisation de la fonction logit, ce qu’on cherche à ajuster avec la fonction coût (la courbe sigmoide ou la droite ax+b avec nos paramètres ?), etc
J’ai cru comprendre que c’était lié au fait qu’on était sur des probabilités et que dans ce cas on ne cherche pas à utiliser la méthode des moindres carrés mais l’estimation du maximum de vraisemblance, etc
En plus, de ce que je sais l’algorithme de régression logistique est utilisé dans la fonction d’activation dans le deep learning. Donc ça pourrait être un plus d’avoir ces explications.
Ma remarque ci-dessus n’est destinée qu’à ce que ton site soit au top du top parce que vu la qualité de tes tutos, tu ne dois avoir que de bons retours. Avoir des remarques de ce type peut te permettre de voir ce qui peut être à continuer/améliorer.
Encore merci pour tous ces tutoriels et le temps que tu passes pour les mettre à disposition gratuitement !
Honnêtement, vu la qualité de tes tutos sur youtube, ça ne m’étonnerait pas que tu atteignes un nombre d’abonnés à 6 chiffres assez rapidement !
Bonjour Karim et merci beaucoup pour ton commentaire très constructif ! Tes remarques sont très utiles et je t’assures que je vais continuer dans cette voie de vidéos détaillées. Je suis d’accord que le livre contient moins de détails, mais c’était son but. Je répondrais bientôt a tes questions concernant la fonction sigmoïde (et comme tu l’a compris c’est lié au maximum de vraisemblance, et joue un rôle important dans les réseaux de neurones)
Merci pour tes encouragements et a bientôt !
Bonjour Guillaume;
Chose que je n’arrive pas à comprendre dans l’apprentissage supervisé par un modèle KNN c’est:
Que dans un modèle de regression linéaire ou polynomiale on cherche à optimiser l’erreur pour trouver les meilleurs parametres et ce en commencant par des parametres arbitraires pour le modèle choisi, c’est ok. Mais dans les knn, comment choisir mon modele? ou juste annoter les sorties de mes features? ou quoi faire vraiment c le point que je n’arrive pas à comprendre et j’aimerais bien comprendre ça.
Merci beaucoup pour cette série de cours en ML.
Bonjour, le K-Nearest Neighbour est une famille d’algorithmes non paramétrés, c’est-a-dire qu’ils ne développent pas de fonction mathématique avec des coefficients, mais garde juste en mémoire tous les exemples qu’on lui montre.
Bonjour Guillaume,
Merci beaucoup pour tes explications qui m’ont été très utiles étant débutante sur le domaine.
J’ai une question stp, je n’arrive pas à comprendre la signification concrète du paramètre Alpha. Correspond-t-il à une distance sur le graphe que tu as présenté ?
Merci beaucoup et bonne continuation.
Il s’agit du pas que l’on fait lors de la descente de gradient. C’est semblable la la taille du pas que vous feriez en descendant une montagne.
Bonjour Guillaume ,
Merci beaucoup pour cette série de cours , Je trouve quelques difficultés à utilise la méthode de gradient pour régression linéaire sur Matlab .
Bonjour, je vous invite a nous rejoindre sur discord si vous avez des questions, nous y répondrons ! 🙂
En statistique, alpha est aussi appelé “coefficient de la pente”.
Bonjour,
Je réitère mon post de Youtube tellement c’est bon :
============================
Cette formation : c’est que du bonheur.
Enfin une personne très compétente qui prend plaisir à partager son savoir : et en plus qui le fait bien car très pédagogue.
Je passe presque les vidéos en boucle tellement c’est passionnant. Enfin l’Informatique basé sur des Mathématiques telle qu’on l’apprend à l’Université. Aujourd’hui trop de gens pensent être informaticien et ces personnes ne basent pas leur travaux sur les mathématiques : ils n’ont rien compris et cela donne cette pléthore d’applications qui ne fonctionnent pas (manque de performance, bugs, etc.).
Que tous ceux qui se disent spécialistes et qui font des formations (souvent payantes) prennent de la graine.
Merci encore et encore.
============================
Merci beaucoup pour les explications , elles sont claires surtout pour une débutante comme moi.
Bonjour,
Vous devriez être professeur en fac pour donner envie aux étudiants de faire des études scientifiques, avec vous, les choses compliquées s’énoncent simplement, c’est très fort Tout au long de mes études universitaires j’ai toujours eu l’impression que c’était l’inverse, tout est compliqué, c’est un charabia souvent incompréhensible qui en décourage plus d’un.
C’est un plaisir de suivre vos vidéos, dans mon cursus j’ai suivi des cours sur les réseaux connexionnistes, la reconnaissance des formes et autre sans conviction et la j’avoue (20 ans après) que j’aurais aimé avoir un enseignant de votre calibre. Merci encore
à la lecture de vos articles.
Merci beaucoup, je vois tout a fait de quoi vous voulez parler car j’ai moi aussi connu cela, c’est pour cette raison que je me donne a fond pour essayer de simplifier, d’expliquer, de marquer les esprits, pour le bien des gens. Je préfère donner de la valeur plutôt que d’avoir un discours ultra compliqué pour passer pour quelqu’un d’intelligent.
A Bientôt !
Franchement rien à dire, je suis content d’être tombé sur tes vidéos. Ton livre apprendre le ML en une semaine, je l’ai fini en une journée avec bien sur les examples de codes. C’est bref mais instructif. Continue dans ce sens là.
excellent bravooooooo. magnifique merci beaucoup pour l’explication.