Les Matrices : Définition et utilité
Une matrice, c’est un tableau de nombre qui obéit à des règles d’algèbre linéaire un peu particulières. On s’en sert pour effectuer des opérations sur des paquets de nombres, qui, en général, ont tous un lien en commun les uns avec les autres.
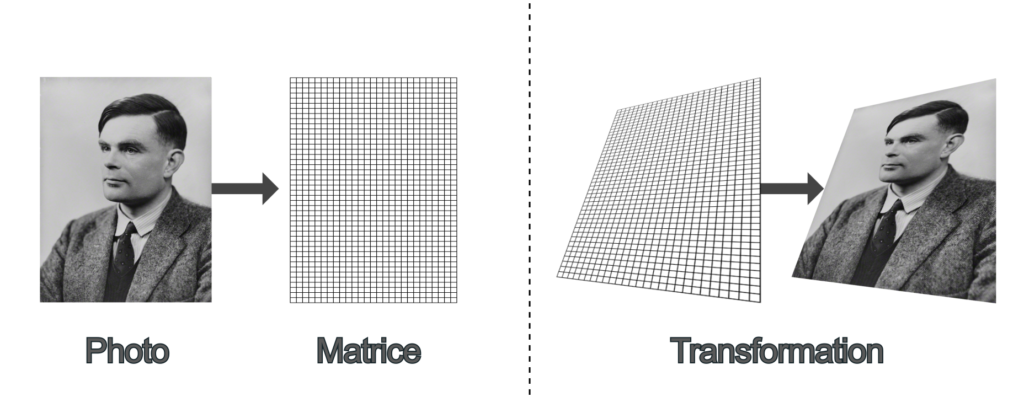
Par exemple, on peut placer tous les pixels d’une photo dans une matrice, dans le but de transformer la photo (changer sa luminosité ou la déformer) en appliquant une seule transformation sur cette matrice. Procéder ainsi est bien plus efficace que de modifier la valeur de chaque pixel l’un après l’autre.
En Machine Learning, les matrices sont utilisées pour manipuler d’une seule traite toutes les données de notre Dataset. Avec elles, on peut calculer les prédictions d’un modèlef(x) = ax + b ainsi que la fonction coût et les gradients sur tout le Dataset, plutôt que point par point.
La dimension d’une matrice
On dit qu’une matrice est de dimension (m \times n) lorsqu’elle a m lignes et n colonnes.
Par exemple la matrice A = \begin{bmatrix} 1 & 2\\ 3 & 4\\ 5 & 6 \end{bmatrix} est une matrice de dimension (3 \times 2).
Notez sur feuille les dimensions de vos matrices est très important pour éviter les erreurs de calcul dans vos programmes de Machine Learning.
La transposée d’une matrice
Par définition, la transposée d’une matrice se note A^T et représente la matrice que l’on aurait renversée sur elle-même.
Par exemple, la transposée de la matrice
A = \begin{bmatrix} 1 & 2\\ 3 & 4\\ 5 & 6 \end{bmatrix}
donne
A^T = \begin{bmatrix} 1 & 3 & 5\\ 2 & 4 & 6\end{bmatrix}
On remarque que les dimensions de la matrice transposée sont « basculées » : on passe d’une matrice A (3 \times 2) à une matrice A^T (2 \times 3).
Addition et soustractions des matrices
Pour additionner ou soustraire deux matrices ensembles, la règle est simple : elles doivent toutes deux avoir les mêmes dimensions. C’est en fait assez intuitif : on ne peut pas additionner une matrice (2 \times 3) avec une matrice (2 \times 2).
\begin{bmatrix} a & b & c\\ d & e & f\end{bmatrix} + \begin{bmatrix} g &h \\i&j \end{bmatrix} = erreur
Le calcul est lui aussi très intuitif : il s’agit simplement d’additionner (ou de soustraire) chaque élément de chaque matrice pour obtenir le résultat. Le résultat a donc également les mêmes dimensions que les matrices du calcul :
\begin{bmatrix} a & b & c\\ d & e & f\end{bmatrix} + \begin{bmatrix} g & h & i\\ j & k & l\end{bmatrix} = \begin{bmatrix} a+g & b+h & c+i\\ d+j & e+k & f+l\end{bmatrix}
Dans la pratique, la librairie Numpy permet d’étendre les dimensions de vos matrices lorsque celles-ci ont une dimension de 1 sur un de leurs axes. C’est ce qu’on appelle le broadcasting.
\begin{bmatrix} a & b & c\\ d & e & f\end{bmatrix} + \begin{bmatrix} g \\ h \end{bmatrix} = \begin{bmatrix} a + g &b+g&c+g \\ d+h &e+h&f+h \end{bmatrix}
Produit matriciel
Pour faire le produit A.B, il faut que le nombre de colonnes dans A soit égal au nombre de lignes dans B. Si A (m \times n) et B (n \times z) alors le résultat A.B (m \times z). Le dessin suivant aide à y voir plus clair :
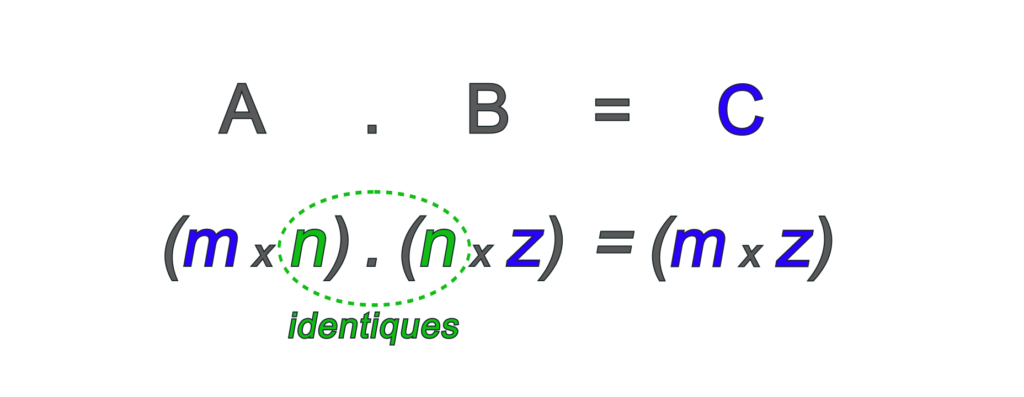
Concernant le calcul, si l’on a :
A.B = \begin{bmatrix} a & b\\ c & d \end{bmatrix} . \begin{bmatrix} e &f &g \\ h&i&j \end{bmatrix} = \begin{bmatrix} ... &... \\...&... \end{bmatrix}
Alors pour calculer le premier élément (ligne 1, colonne 1), on combine la ligne 1 de A avec la colonne 1 de B pour avoir :
A.B = \begin{bmatrix} a & b\\ . & . \end{bmatrix} . \begin{bmatrix} e &. &. \\ h&.&. \end{bmatrix} = \begin{bmatrix} ae + bh &... \\...&... \end{bmatrix}
Puis, pour calculer l’élément (ligne 1, colonne 2), on combine la ligne 1 de A avec la colonne 2 de B :
A.B = \begin{bmatrix} a & b\\ . & . \end{bmatrix} . \begin{bmatrix} . &f &. \\ .&i&. \end{bmatrix} = \begin{bmatrix} ... & af + bi \\...&... \end{bmatrix}
On continue ainsi en suivant le même schéma…
Manipuler des matrices avec Numpy
Numpy est le package de Python qui permet de créer et manipuler des matrices. Dans le code qui suite nous allons créer les matrices suivantes:
A = \begin{bmatrix} 1 & 2\\ 3 & 4\\ 5 & 6 \end{bmatrix}
B = A^T de dimension (2 \times 3)
C = \begin{bmatrix} 1 & 1\\ 1 & 1\\ 1 & 1 \end{bmatrix}
D = A + C
E = A.B de dimension (3 \times 3)
Au passage, nous afficherons les dimensions de chaque matrice avec “.shape”
Note: pour écrire un commentaire dans Python, on commence la ligne par le symbole #
# la ligne suivante charge le package numpy pour accéder aux fonctionnalités
import numpy as np
# Création d'une matrice (3, 2)
A = np.array([[1, 2], [3, 4], [5, 6]])
print('A =', A) # afficher la matrice A
# afficher les dimensions de A
print('dimensions de A:', A.shape)
# Transposée de A
B = A.T
print('B =',B)
print('dimensions de B :', B.shape)
# Création d'une matrice B remplie de "1"
C = np.ones((3, 2))
# addition de A par B
D = A + C
print('C =', C)
print('dimensions de C:', C.shape)
# mutiplication de A (3, 2) par B (2, 3)
E = A.dot(B)
print('E =', E)
print('dimensions de E:',E.shape)
Bonjour, j’ai terminé les 5 chapitres et ils sont assez bien illustrés je trouve. pour un debutant comme moi dans le domaine la compréhension était au rendez vous,merci. À chaque lecture mon appétit pour écrire un programme de machine learning grandissait.
Je suis ravi de l’apprendre ! un grand merci pour votre retour. RDV sur YouTube pour les programmes 🙂
J’ai hâte de voir la suite. Aussi merci pour le livre.
Merci pour votre commentaire 🙂 La suite arrivera vite ! Je fais de mon mieux pour publier chaque semaine sur YouTube ET sur le site.
De rien pour le livre, vous pouvez le partager avec un(e) ami(e) si vous le désirez 🙂
Salut Guillaume. Cette formation est vraiment SUPER !!! Très claire et donnée avec beaucoup de pédagogie. Un GRAND merci à toi. En tant que matheux lorsque j’étais jeune, j’ai très bien compris les formules de calcul de la fonction coût. Je compte suivre tous tes cours & vidéos car je suis en phase de conversion. J’ai 61 ans. J’ai été ingénieur informatique pendant 37 ans (R&D, Bases de Données, langages C, SQL, …) . J’ai connu l’IA dans ses débuts dans les années 80, mais comme tu le sais la puissance des machines de l’époque n’ont pas permi le lancement réel de la téchnologie. Aujourd’hui, je quitte l’entreprise (plan social) et je compte me mettre à mon compte. J’ai adoré le domaine de Machine Learning et je vais aller jusqu’au bout dans les formations en espérant pouvoir participer à des projets même si cela semble être réservé principalement à des jeunes 🙂
Milles mercis Abderrazak et bravo pour votre motivation et votre enthousiasme. J’espère sincèrement que mes formations vous permettront d’atteindre vos buts !
A bientôt !
Salut, ligne 4 tu écris # Création d’une matrice (2, 3)
C’est pas une matrice (3,2) à la place ? 🙂
Salut Arnaud, tu as tout a fait raison je corrige ca ! 🙂
Bien expliqué
tres bien expliqueé , bravo tu me facilite la vie 🙂
Très bon cours, svp je veux la suite je suis bien intéressée par ce domaine. merci bcp 🙂
Très bien expliquée; Cette formation est vraiment super; Très claire et donnée avec beaucoup de pédagogie.
Bonjour Guillaume, à la ligne 17 tu indiques la création d’une matrice B remplie de “1” et donc je ne comprends pas ligne suivante :
c = np.ones(3,2) –> la variable est c (aurais-je louper quelque chose ?)
Je te remercie
Cordialement,
Philippe
Bonjour Guillaume,
j’ai trouvé ma réponse.
Cordialement