Cet article est une introduction à Numpy, le package python permettant de générer des tableaux multi-dimensionnel. Numpy est indispensable dans la pratique du Machine Learning et de la Data Science.

Numpy ndarray: Le tableau à N-Dimensions

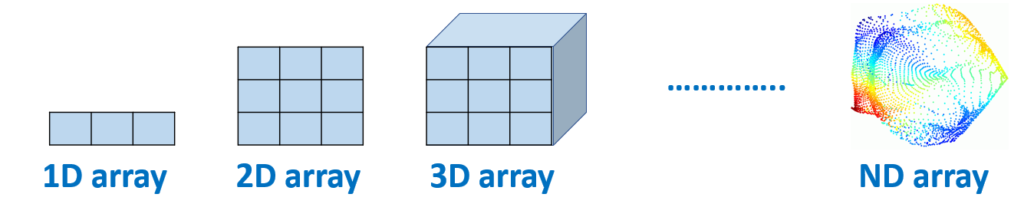
Au cœur de Numpy se trouve un objet très puissant: Le tableau à N-Dimensions (ndarray).

Cet object permet d’effectuer beaucoup d’actions mathématiques avancées, il permet de contenir une infinité de données, et est très rapide d’exécution.

En ingénierie, machine learning et Data Science, on travaille le plus souvent avec des tableaux à 2 dimensions (dataset, image, matrice). Parfois à 3 dimensions (pour une image en couleur, qui contient les couches Rouge, Vert, Bleu)

Générateurs de tableaux Numpy

A = np.zeros((2, 3)) # tableau de 0 aux dimensions 2x3
B = np.ones((2, 3)) # tableau de 1 aux dimensions 2x3
C = np.random.randn(2, 3) # tableau aléatoire (distribution normale) aux dimensions 2x3
D = np.random.rand(2, 3) # tableau aléatoire (distribution uniforme)

E = np.random.randint(0, 10, [2, 3]) # tableau d'entiers aléatoires de 0 a 10 et de dimension 2x3

Il est d’ailleurs possible de choisir le type de données qu’on souhaite utiliser pour notre tableau à l’aide du paramètre dtype. Celui-ci peut s’avérer crucial pour des codes puissants et performants.

A = np.ones((2, 3), dtype=np.float16)
B = np.eye(4, dtype=np.bool) # créer une matrice identité et convertit les éléments en type bool.

La classe du tableau à N-Dimensions (ndarray) propose plusieurs attributs et méthodes. Voici les plus utiles, qu’il faut absolument connaitre !

Attributs importants de ndarray

A = np.zeros((2, 3)) # création d'un tableau de shape (2, 3)

print(A.size) # le nombre d'éléments dans le tableau A
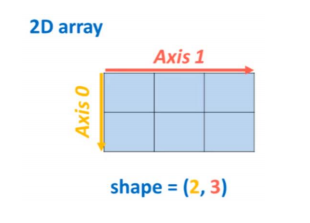
print(A.shape) # les dimensions du tableau A (sous forme de Tuple)

print(type(A.shape)) # voici la preuve que la shape est un tuple

print(A.shape[0]) # le nombre d'éléments dans la premiere dimension de A

Méthodes importantes de ndarray

A = np.zeros((2, 3)) # création d'un tableau de shape (2, 3)

A = A.reshape((3, 2)) # redimensionne le tableau A (3 lignes, 2 colonnes)
A.ravel() # Aplatit le tableau A (une seule dimension)
A.squeeze() # élimine les dimensions "1" de A.

Indexing et Slicing dans un Tableau Numpy

Lorsqu’on travaille sur un tableau Numpy (le plus souvent 2D), il est important de pouvoir y naviguer facilement afin de pouvoir manipuler les données. Pour cela, on se déplace sur un axe à la fois, ce qui nous amène à changer notre position seulement en fonction de ce même axe.

Indexing

Comme pour les listes, on choisit d’accéder à un élément particulier du tableau en indiquant un index pour cet élément.

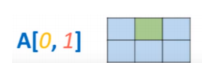
A = np.array([[[1, 2, 3], [4, 5, 6]])

print(A[0, 1]) # ligne 0, colonne 1

Slicing

Dans le cas du slicing, on choisit plutôt d’accéder à plusieurs éléments d’un même axe du tableau. On parlera souvent de sous-ensemble (subset). Il faudra donc indiquer un index de début et un index de fin pour chaque dimension de notre tableau

Note: L’index de fin n’est jamais compris dans l’opération de Slicing.

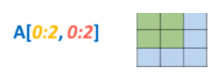
A = np.array([[[1, 2, 3], [4, 5, 6]])

print(A[0:2, 0:2]) # ligne 0 et 1, colonne 0 et 1

Sur Internet, il est courant de voir des opérations de Slicing “implicites”, dans lesquelles seul 1 index est donné. Ceci extrait toute la ligne correspondante à cet index (voir l’exemple ci-dessous). Pour plus de clarté, je recommande de toujours utiliser une syntaxe explicite dans vos codes.

A = np.array([[[1, 2, 3], [4, 5, 6]])

print(A[1,:] # imprime toute la ligne 1, de façon explicite

print(A[1]) # imprime toute la ligne 1, mais cette syntax n'est pas idéale

A présent, intéressons-nous à une technique très utilisée en Data Science : Le Boolean Indexing.

Boolean Indexing

Lorsqu’on soumet un test Booléen sur Un tableau Numpy (par exemple A < 5) alors Python produit un tableau Numpy de dtype bool et de même dimension que le tableau A. Ce tableau est appelé masque booléen.

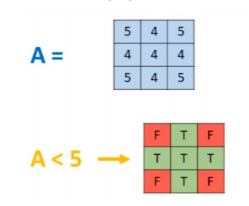
Un masque booléen peut être utilisé en tant que filtre pour réaliser une opération de boolean Indexing : si un élément respecte une condition donnée (bool = True) alors il est sélectionné pour faire parti du sous-ensemble résultat.

Cette technique s’avère très utile en analyse de données pour filtrer ou convertir les valeurs d’un tableau lorsque celle-ci sont inférieures ou supérieures à un certain seuil.

A = np.array([[[1, 2, 3], [4, 5, 6]])

print(A<5) # masque booléen

print(A[A < 5] # sous-ensemble filtré par le masque booléen

A[A<5] = 4 # convertit les valeurs sélectionnées.
print(A)

Mathématiques avec Numpy

Mathématiques de Base

Faire des mathématiques sur Numpy n’est pas spécialement difficile. En effet, Numpy regorge d’une multitude de fonctions pour faire des statistiques et même de l’algèbre linéaire.

La classe ndarray elle-même contient la plupart des fonctions mathématiques de bases: sommes, produits, moyennes, écart types, etc. Il suffit d’utiliser les quelques méthodes suivantes, chacune pouvant être limitée à un des axes du tableau Numpy

A = np.array([[[1, 2, 3], [4, 5, 6]])

print(A.sum()) # effectue la somme de tous les éléments du tableau
print(A.sum(axis=0) # effectue la somme des colonnes (somme sur éléments des les lignes)
print(A.sum(axis=1) # effectue la somme des lignes (somme sur les éléments des colonnes)
print(A.cumsum(axis=0) # effectue la somme cumulée

print(A.prod() # effectue le produit
print(A.cumprod() # effectue le produit cumulé

print(A.min() # trouve le minimum du tableau
print(A.max()) # trouve le maximum du tableau

print(A.mean()) # calcul la moyenne
print(A.std()) # calcul l'ecart type,
print(A.var()) # calcul la variance

Parmi ces méthodes, on trouve également la méthode sort() qui permet de trier un tableau, mais plus utile encore : la méthode argsort()

Numpy Argsort()

Argsort() retourne les index dans l’ordre de tri du tableau, sans modifier ce dernier. Ces index peuvent ensuite être utilisés pour trier toute autre séquence, selon l’ordre du tableau originel.

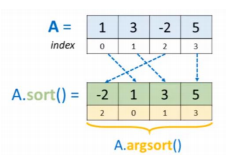
Par exemple, il est possible de trier toute un tableau A en fonction d’une des colonnes de A !

A = np.random.randint(0, 10, [5, 5]) # tableau aléatoire
print(A)

print(A.argsort()) # retourne les index pour trier chaque ligne du tableau 

print(A[:,0].argsort()) # retourne les index pour trier la colonne 0 de A

A = A[A[:,0].argsort(), :] # trie les colonnes du tableau selon la colonne 0.

Numpy Statistics

Au delà des méthodes présentes dans la classe ndarray, Numpy propose beaucoup de fonctions mathématiques plus avancées. Il est possible de faire des statistiques, de l’algèbre linéaire, des transformation de Fourier, etc…

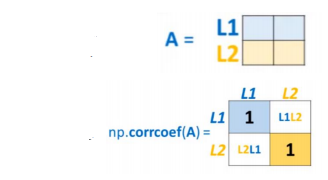
Les routines spécifiques aux statistiques sont tout documentées ici. On y retrouve les moyennes, variances, écart type, mais également de quoi calculer des corrélations et des histogrammes. Parmi ces routines, je recommande de retenir la fonction corrcoef(), avec laquelle on peut calculer la corrélation de Pearson entre les différentes lignes ou colonnes d’un tableau Numpy.

B = np.random.randn(3, 3) # nombres aléatoires 3x3

# retourne la matrice de corrélation de B
print(np.corrcoef(B))

# retourne la matrice de corrélation entre les lignes 0 et 1 de B
print(np.corrcoef(B[:,0], B[:, 1]))

# sélectionne la corrélation entre ligne 0 et ligne 1
print(np.corrcoef(B[:,0], B[:, 1][0,1]))

Statistiques avec NaN

En Data Science, il est courant d’avoir des données manquantes dans un Dataset, celles-ci se manifestent alors sous la forme de valeur NaN dans un tableau Numpy. Dans ces conditions, il n’est pas possible de faire des calculs statistiques. C’est pourquoi Numpy propose des fonctions telles que nanmean(), nanstd() et nanvar() qui permettent d’effectuer ces calculs tout en ignorant les valeurs NaN.

A = np.random.randn(5, 5)
A[0, 2] = np.nan # insere un NaN dans la matrice A

(np.isnan(A).sum()/A.size) # calcule la proportion de NaN dans A

print(np.nanmean(A)) # calcule la moyenne de A en ignorant les NaN

Algèbre Linéaire avec Numpy

Numpy permet également de faire de l’algèbre linéaire grâce aux routines disponibles dans le package numpy.linalg. Les routines qui suivent comptent parmi les plus importantes, et permette de calculer le déterminant d’une matrice, d’inverser une matrice, et de calculer ces vecteurs propres et valeurs propres.

A = np.ones((2,3))
B = np.ones((3,3))

print('transpose', A.T) # transposé de la matrice A (c'est un attribut de ndarray)

print('produit A.B', A.dot(B)) # produit matriciel A.B


A = np.random.randint(0, 10, [3, 3])

print('det', np.linalg.det(A)) # calcule le determinant de A
print('inv A', np.linalg.inv(A)) # calcul l'inverse de A

val, vec = np.linalg.eig(A)
print('valeur propre', val) # valeur propre
print('vecteur propre', vec) # vecteur propre

Broadcasting avec Numpy

Habituellement, quand on cherche à effectuer une opération mathématique entre 2 tableaux dans un langage tel que le C++ (par exemple les additionner ensemble) il faut travailler avec des boucles for afin d’accéder aux différents éléments de ces tableaux (et les additionner ensemble)

Avec Numpy, tout est beaucoup plus simple ! Ce système d’itération est déjà implémenté à l’intérieur de la librairie (via le langage C). Ainsi, pour faire l’addition des éléments entre un tableau A et tableau B, il suffit d’écrire A + B.

Sur le graphique ci-dessus, les tableaux A et B sont de mêmes dimensions (2×3). Cette condition peut sembler nécessaire pour effectuer une addition sur chacun de leur élément, mais elle ne l’est pas ! Une technique appelée Broadcasting permet d’étendre les dimensions d’un tableau (lorsque celles-ci sont égales à 1) pour couvrir les dimensions de l’autre tableau.

Numpy Broadcasting : Les Régles et exemples

Pour effectuer une opération mathématique sur 2 tableaux Numpy, c’est simple: Il faut qu’ils aient les mêmes dimensions, et si ce n’est pas le cas, le Broadcasting peut étendre toute dimension égale à 1 pour couvrir la dimension équivalente de l’autre tableau. Voici quelques exemples accompagnés d’illustrations :

A = np.ones((2, 3))
B = 3
print(A+B) # résultat 1

A = np.ones((2, 3))
B = np.ones((2, 1)) # B a une colonne, elle sera étendu sur les trois colonnes de A
print(A+B) # résultat 2

A = np.ones((2, 3))
B = np.ones((2, 2))

print(A + B) # ERREUR ! Broadcasting incompatible

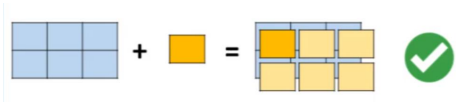
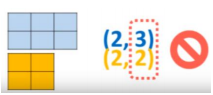
Attention ! Le Broadcasting réserve souvent de mauvaises surprises quand vous oubliez de dimensionner vos tableaux de façon explicite: (3, 1) au lieu de (3,). Par exemple, additionner un tableau A de dimension (3, 1) avec un tableau de dimension (3, ) ne donnera pas un résultat de dimension (3, 1), mais un résultat de dimension (3, 3) (plus de détails dans la vidéo du dessus)

Numpy : Le Bilan

Numpy est le package fondamental pour faire du calcul scientifique avec Python. Tous les autres packages importants en Machine Learning (Pandas, Matplotlib, Sklearn) sont construits sur la base de Numpy. Il est indispensable de bien maîtriser les fonctions de bases présentées dans cet article pour être capable de générer des tableaux, les manipuler (selon leur lignes et leur colonnes) et effectuer quelques opérations mathématiques dessus.