Dans cet article, nous allons développer un algorithme de descente de gradient pour résoudre un problème de régression linéaire avec Python et sa librairie Numpy. Dans la pratique, les Data Scientists utilisent le package sklearn, qui permet d’écrire un tel code en 4 lignes, mais ici nous écrirons chaque fonction mathématique de façon explicite, ce qui est un très bon exercice pour améliorer votre compréhension du Machine Learning.

Importer les packages Numpy et Matplotlib.pyplot

Avant toute chose, il est nécessaire d’importer les packages Numpy et Matplotlib.pyplot. Numpy permet de créer des matrices et effectuer des opérations mathématiques. Matplotlib permet de créer des graphiques pour observer facilement notre dataset ainsi que le modèle construit à partir de celui-ci.

import numpy as np
import matplotlib.pyplot as plt

Génération d’un dataset (x, y) linéaire

Avec la fonction linspace de Numpy, nous créons un tableau de données (x, y) qui présente une tendance linéaire. La fonction random.randn permet d’ajouter un “bruit” aléatoire normal aux données. Pour effectuer un calcul matriciel correct, il est important de confier 2 dimensions (100 lignes, 1 colonne) à ces tableaux en utilisant la fonction reshape(100, 1)

np.random.seed(0) # pour toujours reproduire le meme dataset

n_samples = 100 # nombre d'echantillons a générer
x = np.linspace(0, 10, n_samples).reshape((n_samples, 1))
y = x + np.random.randn(n_samples, 1)


plt.scatter(x, y) # afficher les résultats. X en abscisse et y en ordonnée
plt.show()

Une fois le dataset généré, il faut ajouter une colonne de biais au tableau X, c’est-à-dire un colonne de 1, pour le développement du futur modele linéaire f(x) = a \times x + b \times 1, puis initialiser des paramètres (a,b) dans un vecteur theta \theta.

# ajout de la colonne de biais a X
X = np.hstack((x, np.ones(x.shape)))
print(X.shape)

# création d'un vecteur parametre theta
theta = np.random.randn(2, 1)
print(theta)

Développement des fonctions de Descente de gradient

Pour développer un modèle linéaire (ou polynomial !) avec la déscente de gradient, il faut implémenter les 4 fonctions clefs suivantes :

• la fonction de notre modèle : f(x) = X.\theta
• la fonction Coût : J(\theta) = \frac{1}{2m} \sum (X.\theta - Y)^2
• le gradient : \displaystyle \frac{\partial J(\theta)}{\partial \theta} = \frac{1}{m} X^T.(X.\theta – Y)
• la descente de gradient : \theta = \theta - \alpha \times \frac{\partial J(\theta)}{\partial \theta}

def model(X, theta):
    return X.dot(theta)

def cost_function(X, y, theta):
    m = len(y)
    return 1/(2*m) * np.sum((model(X, theta) - y)**2)

def grad(X, y, theta):
    m = len(y)
    return 1/m * X.T.dot(model(X, theta) - y)

def gradient_descent(X, y, theta, learning_rate, n_iterations):
    # création d'un tableau de stockage pour enregistrer l'évolution du Cout du modele
    cost_history = np.zeros(n_iterations) 
    
    for i in range(0, n_iterations):
        theta = theta - learning_rate * grad(X, y, theta) # mise a jour du parametre theta (formule du gradient descent)
        cost_history[i] = cost_function(X, y, theta) # on enregistre la valeur du Cout au tour i dans cost_history[i]
        
    return theta, cost_history

Entrainement du modèle

Une fois les fonctions ci-dessus implémentées, il suffit d’utiliser la fonction gradient_descent en indiquant un nombre d’itérations ainsi qu’un learning rate, et la fonction retournera les paramètres du modèle après entrainement, sous forme de la variable theta_final.

Vous pouvez ensuite visualiser votre modèle grâce à Matplotlib.

n_iterations = 1000
learning_rate = 0.01

theta_final, cost_history = gradient_descent(X, y, theta, learning_rate, n_iterations)

print(theta_final) # voici les parametres du modele une fois que la machine a été entrainée

# création d'un vecteur prédictions qui contient les prédictions de notre modele final
predictions = model(X, theta_final)

# Affiche les résultats de prédictions (en rouge) par rapport a notre Dataset (en bleu)
plt.scatter(x, y)
plt.plot(x, predictions, c='r')
plt.show()

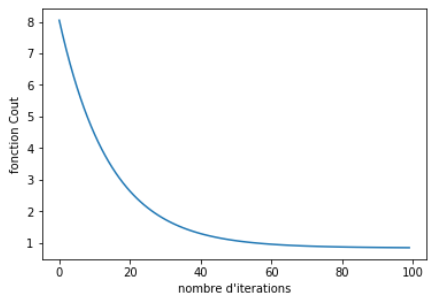
Pour finir, vous pouvez visualiser l’évolution de la descente de gradient en créant un graphique qui trace la fonction_cout en fonction du nombre d’itération. Si votre descente de gradient a bien fonctionné, vous devez obtenir une courbe qui diminue progressivement jusqu’à converger vers un certain minimum. Si vous n’observez pas de stabilisation, alors cela signifie que le modèle n’a pas terminé son apprentissage et qu’il faut soit augmenter le nombre d’itérations de la descente de gradient ou bien le pas (learning_rate).

plt.plot(range(n_iterations), cost_history)
plt.show()