Scipy est le package scientifique le plus important de Python. Construit sur la base de Numpy et développé en C/C++, Scipy contient un large panel de fonctions mathématiques et scientifiques très performantes. Pour cette raison, de nombreux ingénieurs, data scientists, et chercheurs l’utilisent dans leurs projets. Dans ce tutoriel, nous allons voir quelques uns des modules les plus utiles pour effectuer des opérations d’interpolation, d’optimisation, et de traitement du signal. Si ces domaines vous semblent trop complexes, ne vous en faites pas, Scipy est très facile à prendre en main.

Interpolation de signal avec Scipy

L’interpolation de signal consiste à générer un signal de fréquence plus élevée que le signal d’origine, en reliant les différents point du signal d’origine avec une des méthodes suivantes :

• Interpolation linéaire (vous tracez une droite entre chaque point)
• Interpolation quadratique (connecte les points avec un polynôme de degré 2)
• Interpolation cubique (connectes les points avec un polynôme de degré 3)
• Interpolation du plus proche voisin (connecte les points en escalier)

Exemple d’application : un capteur collecte la température d’un four une fois par seconde, mais vous avez besoin de ce signal 10 fois par seconde. C’est l’occasion parfaite d’utiliser le module interpolate de scipy, qui vous permet de générer une telle interpolation avec la fonction interp1d

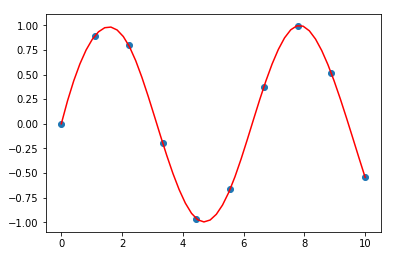
import numpy as np
import matplotlib.pyplot as plt


# Création d'un Dataset
x = np.linspace(0, 10, 10)
y = np.sin(x)

from scipy.interpolate import interp1d

# création de la fonction interpolation f
f = interp1d(x, y, kind='cubic')

# résultats de la fonction interpolation f sur de nouvelles données
new_x = np.linspace(0, 10, 50)
result = f(new_x)

# visualisation avec matplotlib
plt.scatter(x, y)
plt.plot(new_x, result, c='r')
plt.show()
<p>

Attention : Avant d’interpoler un signal, assurez vous que le risque de variation soudaine dans ce signal soit faible. Par exemple : La température d’un four entre chaque seconde évolue à coup sur de façon linéaire, et le risque de variation de température soudaine est très faible, mais ce n’est pas le cas pour toutes les applications...

Note : Scipy vous permet élégamment d’effectuer des interpolations sur des images (en améliorer la résolution) grâce à la fonction interp2d

Optimisation avec Scipy

L’optimisation est une technique qui touche tous les domaines. Tout le monde veut optimiser un produit ou processus, maximiser ses gains, minimiser ses risques, etc.

Le module scipy.optimize contient de nombreux outils dédiés aux problèmes d’optimisation : Minimisation de fonction, ajustement de courbes, programmation linéaire… Voyons tout de suite la minimisation de fonction (et la vidéo ci-dessus aborde également l’ajustement de courbe)

Minimisation 1D

Minimiser/maximiser une fonction est un problème très courant en ingénierie, science, ou en finance. Cela consiste à trouver le minimum/maximum global d’une fonction sur un domaine d’étude. Pour ça, la méthode de Newton ou la descente de gradient, comptent parmi les techniques les plus populaires. Ces techniques peuvent toutes être implémentées facilement avec la fonction optimize.minimize().

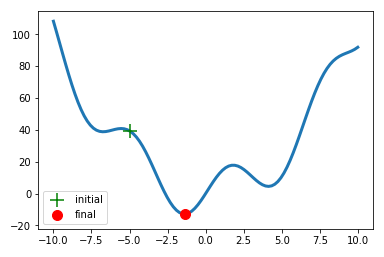
import numpy as np
import matplotlib.pyplot as plt


# Définition d'une fonction a 1 Dimension
def f (x):
    return x**2 + 15*np.sin(x)


# Visualisation de la fonction
x = np.linspace(-10, 10, 100)
plt.plot(x, f(x))

# Définition d'un point x0 pour l'algorithme de minimisation
x0=-5
result = optimize.minimize(f, x0=x0).x # résultat de la minimisation

# Visualisation du résultat

plt.plot(x, f(x), lw=3, zorder=-1) # Courbe de la fonction
plt.scatter(x0, f(x0), s=200, marker='+', c='g', zorder=1, label='initial') # point initial
plt.scatter(result, f(result), s=100, c='r', zorder=1, label='final') # point final
plt.legend()
plt.show()
<p>

Note : Il n’existe pas de fonction maximize() dans scipy car Maximiser une fonction revient à minimiser sa fonction négative. Dans la pratique, nous effectuons donc tout le temps des minimisations.

Minimisation 2D

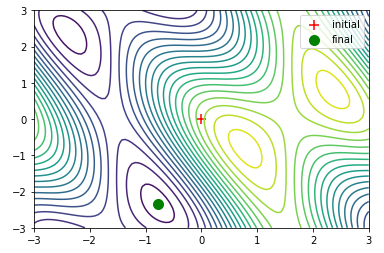
import numpy as np
import matplotlib.pyplot as plt


# Définition d'une fonction 2D. X est un tableau numpy a 2-Dimension
def f (x):
    return np.sin(x[0]) + np.cos(x[0]+x[1])*np.cos(x[0])

# Génération de la fonction sur un espace 2D.
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
x, y = np.meshgrid(x, y)

# Placement d'un point x0 initial aux coordonées (0,0)
x0 = np.zeros((2, 1))

# Minimisation de la fonction
result = optimize.minimize(f, x0=x0).x
print('le minimum est aux coordonées', result) # imprimer le résultat

# Visualisation du résultat
plt.contour(x, y, f(np.array([x, y])), 20) # fonction 2D
plt.scatter(x0[0], x0[1], marker='+', c='r', s=100, label='initial') # Point de départ
plt.scatter(result[0], result[1], c='g', s=100, label='final') # Point final
plt.legend()
plt.show()
<p>

Traitement du Signal avec Scipy

Scipy inclut de nombreux outils pour filtrer et traiter des signaux. L’un d’entre eux, le module fftpack permet d’effectuer des transformations de Fourier pour nettoyer les signaux périodiques, en connaitre les fréquences, et effectuer d’autres opérations associées.

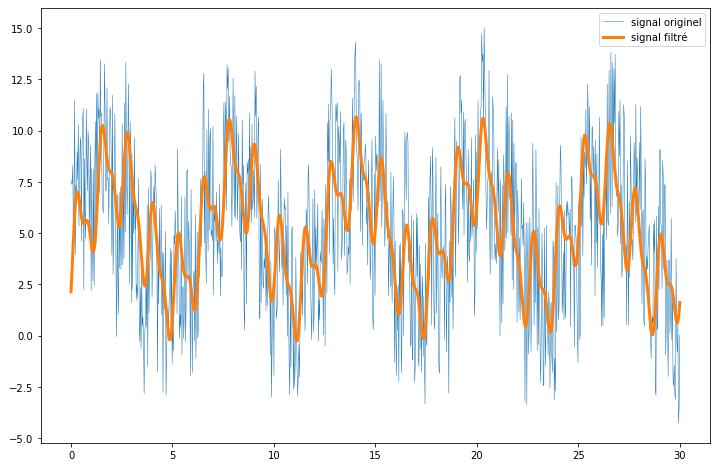
import numpy as np
import matplotlib.pyplot as plt


# Création d'un signal périodique noyé dans du bruit.
x = np.linspace(0, 30, 1000)
y = 3*np.sin(x) + 2*np.sin(5*x) + np.sin(10*x) + np.random.random(x.shape[0])*10


from scipy import fftpack

# création des variables Fourier et Fréquences, qui permettent de construire le spectre du signal.
fourier = fftpack.fft(y)
power = np.abs(fourier) # la variable power est créée pour éliminer les amplitudes négatives
frequences = fftpack.fftfreq(y.size)


# filtre du spectre avec du boolean indexing de Numpy
fourier[power<400] = 0

# Transformation de Fourier Inverse: genere un nouveau signal temporel depuis le spectre filtré
filtered_signal = fftpack.ifft(fourier)

# Visualisation des résultats
plt.figure(figsize=(12, 8))
plt.plot(x, y, lw=0.5, label='signal originel')
plt.plot(x, filtered_signal, lw=3, label='signal filtré')
plt.legend()
plt.show()
<p>